olzdeal.blogg.se - Python code for gauss seidel method

Gauss Seidel Iteration Method C Program.

Gauss Seidel Iteration Method Algorithm.

Jacobi Iteration Method C++ Program with Output.

Power Method (Largest Eigen Value & Vector) Python Program.

Power Method (Largest Eigen Value and Vector) C++ Program.

Power Method (Largest Eigen Value and Vector) C Program.

Power Method (Largest Eigen Value and Vector) Pseudocode.

Power Method (Largest Eigen Value and Vector) Algorithm.

Python Program to Inverse Matrix Using Gauss Jordan.

Matrix Inverse Using Gauss Jordan C++ Program.

Matrix Inverse Using Gauss Jordan C Program.

Matrix Inverse Using Gauss Jordan Method Pseudocode.

Matrix Inverse Using Gauss Jordan Method Algorithm.

Gauss Jordan Method Python Program (With Output).

Gauss Elimination Method Online Calculator.

Gauss Elimination Method Python Program with Output.

Gauss Elimination C++ Program with Output.

Fixed Point Iteration (Iterative) Method Online Calculator.

Fixed Point Iteration (Iterative) Method C++ Program.

Fixed Point Iteration (Iterative) Python Program.

Fixed Point Iteration (Iterative) Method C Program.

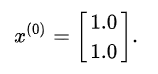
Fixed Point Iteration (Iterative) Method Pseudocode.Fixed Point Iteration (Iterative) Method Algorithm.Secant Method Python Program with Output.Newton Raphson Method Online Calculator.Regula Falsi or False Position Method Online Calculator.Python Program for Regula False (False Position) Method.MATLAB Program for Regula False (False Position) Method.C++ Program for Regula False (False Position) Method.C Program for Regula False (False Position) Method.Pseudocode for Regula Falsi (False Position) Method.Algorithm for Regula Falsi (False Position Method).of iterations but when i take initial guess to be larger than 10 i get larger number of iterations.Ĭan anyone explain.

Now when i am taking initial guess less than 10 i get less no. When initial guess = 0, No of iterations = 350 I have solved this question in python and i am getting following results: Plot the temperature contours as the output. Clearly explain your convergence criterion for the iterations and how it is implemented. Initial guess and comment on the number of iterations required for convergence in each case. Solve the problem using the point-by-point Gauss-Seidel iterative method. Choose a uniform grid size of 0.05 m in both directions. The steady-state temperature distribution within this plate is to be determined for the following imposed boundary conditions: (i) y = 0, T = 100 ̊C, (ii) x = 0, T = 0 ̊C, (iii) y = H, T = 0 ̊C, and (iv) x = L, T = 0 ̊C.

The plate material has constant thermal conductivity. Consider a two-dimensional rectangular plate of dimension L = 1 m in the x direction and H = 2 m in the y direction.